Parsa Kamalipour

RA & TA & Master of Computer Science at Concordia University @ Algorithms & Complexity Lab.

Designing and implementation of:

  • the Red-Black Tree (self-balancing binary search tree)
  • the AVL Tree (self-balancing binary search tree)
  • the Trie Dictionary (k-ary search tree)
  • the Sparse Matrix via Linked List (Linked List)
  • the Rat in the maze problem (Backtracking & Stacks)
DS logo
DS logo

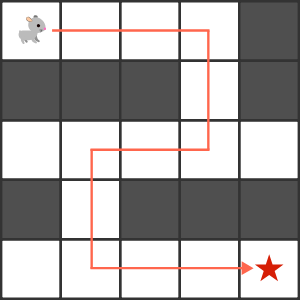
The Rat in the maze problem

  • Code is not available at github at the moment. Let us consider a rat placed at (0, 0) in a square matrix of order N * N. Let us say it has to reach a destination at (N – 1, N – 1). Find all paths the rat can take to reach its destination from its source. There are four directions that the rat can move in: up, down, left, and right. At a cell in the matrix, value 0 indicates that it is blocked and the rat cannot access it, while value 1 indicates that it can pass through it. In a path, no cell can be visited more than once. 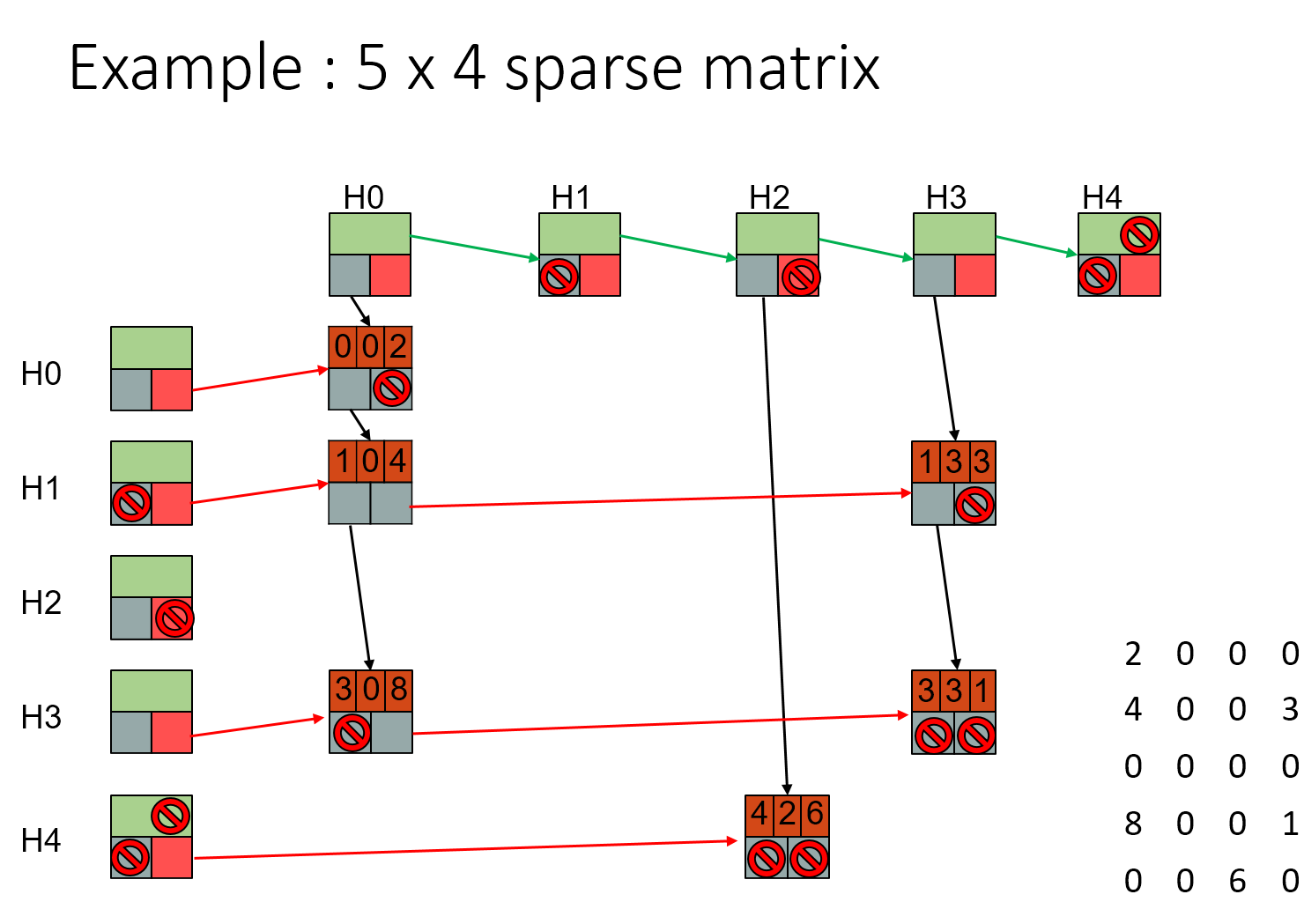image

The Sparse Matrix via Linked List

  • Github repo The usage of a 2D array to represent a sparse matrix wastes a lot of resources because the zeroes in the matrix are rarely used. As a result, we only store non-zero elements instead of storing zeroes with them. This entails using triples to store non-zero elements (Row, Column, value). There are two pointers that lead in two different directions to the following nodes. image

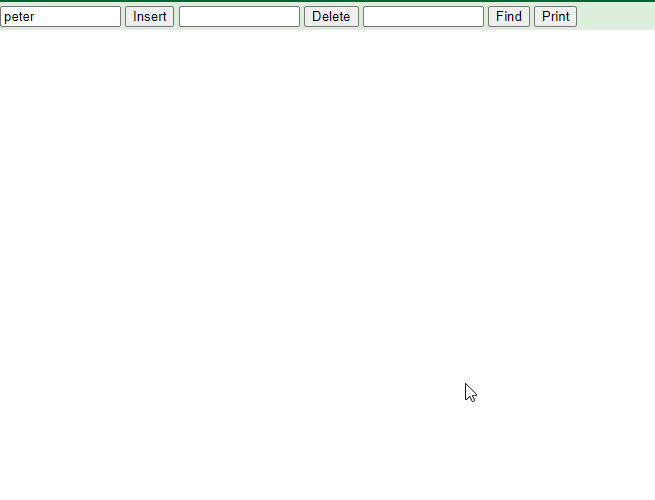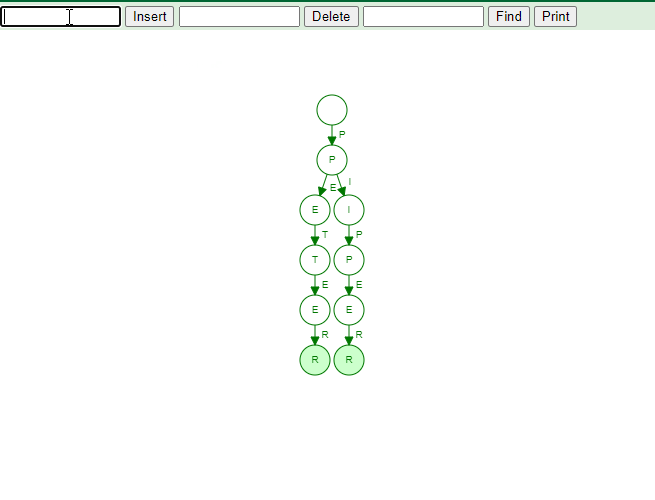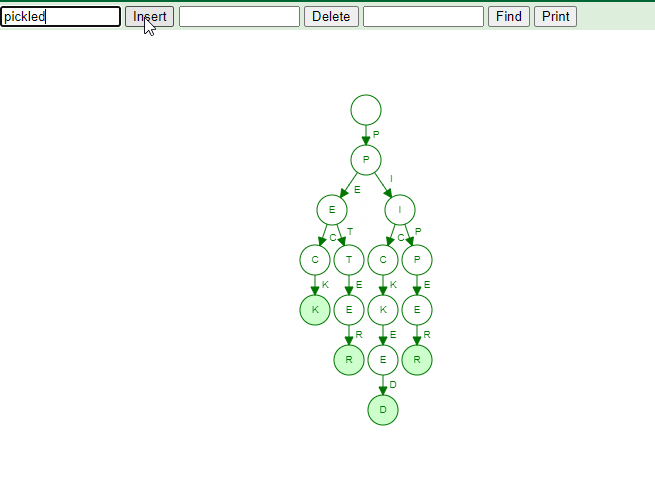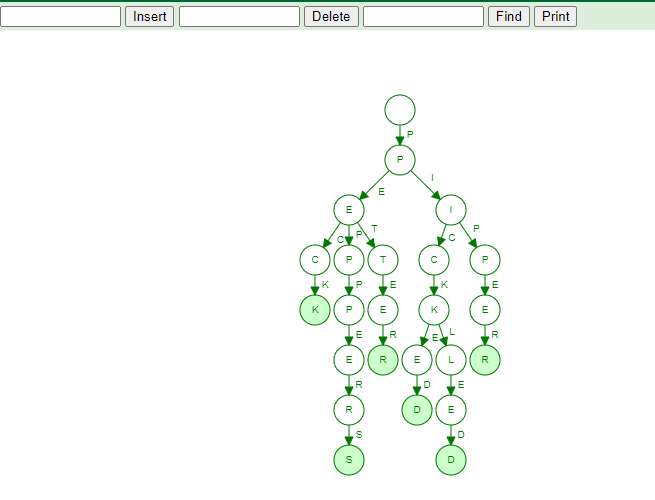
The Trie Dictionary

  • Github repo The word “Trie” is an abbreviation for “retrieval.” The set of strings is stored in a sorted tree-based data structure called a trie. Each node has the same number of pointers as the number of characters in the alphabet. It may use the prefix of a word to look up that word in the dictionary. If we suppose that all strings are made up of the letters a through z from the English alphabet, each trie node can have a maximum of 26 points. The digital tree, or prefix tree, is another name for Trie. The key with which a node is associated is determined by its position in the Trie. 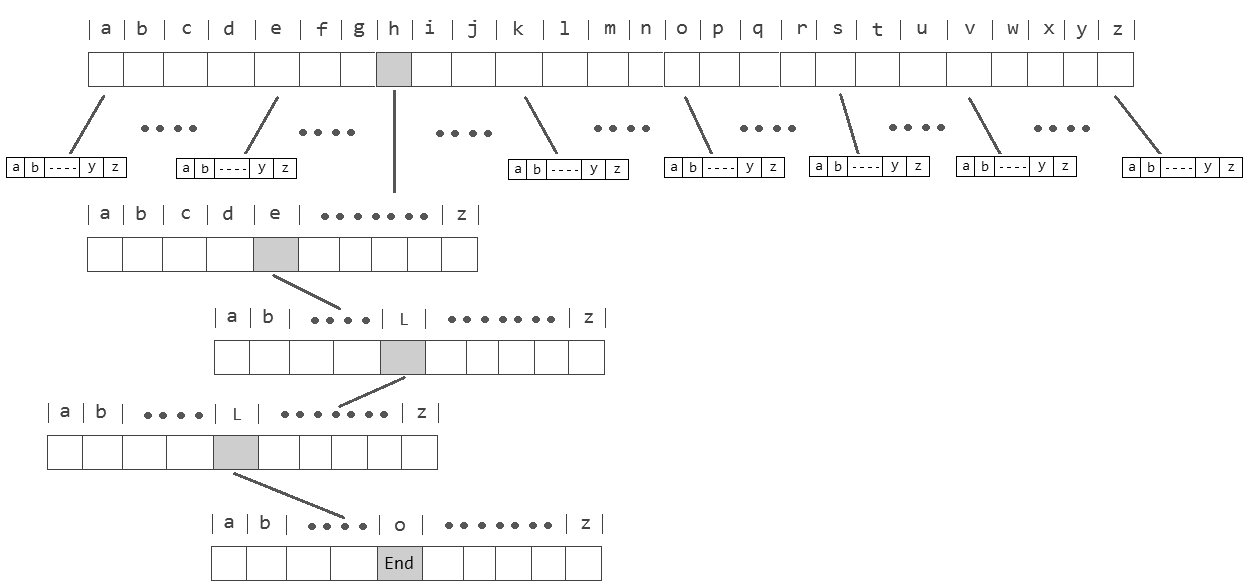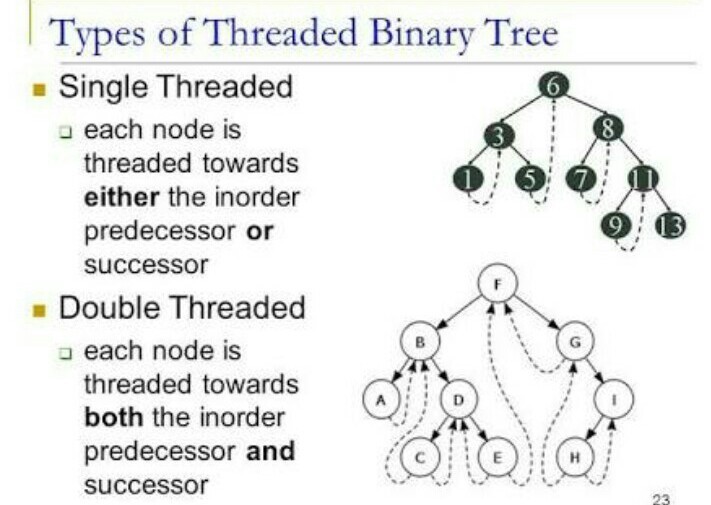image gif

Threaded Binary Tree

  • Code is not available at github at the moment. Threaded binary tree is a simple binary tree but they have a speciality that null pointers of leaf node of the binary tree is set to inorder predecessor or inorder successor. The main idea behind setting such a structure is to make the inorder and preorder traversal of the tree faster without using any additional data structure(e.g auxilary stack) or memory to do the traversal. Each node in a threaded binary tree either contains a link to its child node or thread to other nodes in the tree. image

The AVL Tree

  • Github repo The AVL tree is a self-balancing binary search tree in which each node keeps track of additional information termed a balance factor, which might be -1, 0 or +1. image

The Red-Black Tree

  • Github repo The red-black tree is a self-balancing binary search tree in which each node has an extra bit to indicate whether it is red or black.

Updated: